Zerfallskonstante λ berechnen
Die sogenannte Zerfallskonstante ist für einige Berechnungen von radioaktiven Zerfällen von Bedeutung. Sie beschreibt, wie schnell gewisse Elemente zerfallen. Je schneller ein Element zerfällt, desto größer ist der Wert. Diese Zahl wird benötigt, um beispielsweise die Menge eines radioaktiven Elements nach einer gewissen Zeit zu berechnen. Mehr dazu könnt ihr im Artikel zum Zerfallsgesetz erfahren.
Formelsymbol: λ
Einheit: 1/s
Formel zur Zerfallskonstante
Man kann die Zerfallskonstante mit der Halbwertszeit, oder die Halbwertszeit mit der Zerfallskonstante berechnen (stellt dazu jeweils die Formel mit der Äquivalenzumformung um):

- T1/2 = Halbwertszeit
- λ = Zerfallskonstante
Beispielaufgabe zur Berechnung der Zerfallskonstante
Was ist die Zerfallskonstante des Elements C-14? Die Halbwertszeit beträgt 5730 Jahre. Die Berechnung sieht dann wie folgt aus:

Die Zerfallskonstante hat also den Wert λ=0,000121 1/a. Um nun die Standardeinheit (1/s) der Zerfallskonstante zu erhalten, müsst ihr diesen Wert durch 365∙24∙60∙60=31.536.000s teilen. Denn ein Jahr hat so viele Sekunden.
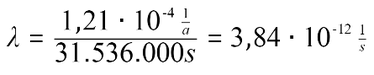
Tabelle mit Halbwertszeiten und Zerfallskonstanten
In dieser Tabelle seht ihr einige ausgewählte Elemente mit ihren Halbwertszeiten und Zerfallskonstanten.
| Element | Halbwertszeit | Zerfallskonstante λ (1/s) |
| Uran-238 | 4,5 ∙ 109 a | 5,0 ∙ 10-18 |
| Plutonium-239 | 2,4 ∙ 104 a | 9,2 ∙ 10-13 |
| Kohlenstoff-14 | 5730 a | 3,9 ∙ 10-12 |
| Radium-226 | 1602 a | 1,35 ∙ 10-11 |
| Polonium-210 | 138 Tage | 5798 ∙ 10-8 |
| Thorium-216 | 26 ms | 26.660 |
